一、样本与总体
前面已提及,医学研究中实际观测或调查的一部分个体称为样本,研究对象的全部称为总体。如作水质检验时从井水或河水中采的水样,临床化验中从病人身上采的血液或其它活体组织标本,是样本;而整个一口井或一条河的某一段所有的水,某病人全身所有的血液或某个组织器官,则是总体。这类总体是具体存在的,但另有些总体却是假想的,只是理论上存在的一个范围。例如试验某一治疗流感新药的疗效,最初接受治疗的一批流感患者,不论数量多少,都只是一个样本。若该药疗效得到肯定,从而加以推广,那么此后凡在相同条件下接受该药治疗的所有流感患者,都属于这个总体。可是当初试用时,这个总体还并不存在,是假想的。
总体包含的观察单位通常是大量的甚至是无限的,在实际工作中,一般不可能或不必要对每个观察单位逐一进行研究。我们只能从中抽取一部分观察单位加以实际观察或调查研究,根据对这一部分观察单位的观察研究结果,再去推论和估计总体情况。如上述某新药治疗流感例子,试验治疗的只是少数有限的病人,而结论却要推广到全体,得出一个该药对所有流感患者之疗效的规律性的认识。所以说,观察样本的目的在于推论总体,这就是样本与总体的辩证关系。
为了使样本能够正确反映总体情况,对总体要有明确的规定;总体内所有观察单位必须是同质的;在抽取样本的过程中,必须遵守随机化原则;样本的观察单位还要有足够的数量。
二、概率
又称机率,是用以描述某事件发生的可能性大小的一个数值。
在自然界和人类社会中,存在着两类不同的现象:①在一定条件下,肯定发生的事件叫做必然事件,肯定不发生的事件叫做不可能事件。如在适当温度湿度下经一定时间孵化,正常受精鸡蛋必然会孵出小鸡来,而石头是不可能孵出小鸡来的。必然事件与不可能事件虽然形式相反,但两者在发生某种结果与否都是确定的,故统称确定性现象。②在基本条件不变的情况下,可能发生的结果有多种,究竟发生哪种结果,事先不能肯定,这类现象叫做随机现象。随机现象的表现结果称为随机事件。如任意抛掷一枚硬币,可能徽花向上也可能币值向上,抛掷前不能肯定,这是一个随机现象,而结果出现“徵花向上”则是一个随机事件。
(一)古典概率 是最简单的随机现象的概率计算。这类随机现象具有两个特征:①在观察或试验中它的全部可能结果只有有限个,譬如为n个,记为E1,E2,…,En,而且这些事件是两两互不相容的,即任何两个事件不能同时发生;②事件E1,E2,…,En的发生或出现是等可能的,即它们发生的概率都一样。古典概率的大部分问题都能形象地用摸球模型来描述。有利于直观地理解概率论的许多基本概念;而且它有着多方面的重要应用,例如工业产品的抽样检查等。
(二)统计概率 上述“事件”是指不能再进行分解或不能由其它事件构成的基本事件。在实际工作中,基本事件的发生并不总是等可能的,而且有时为无穷多个。这样就有必要把古典概率的定义加以推广,从事后经验的角度来理解概率的意义。实践证明,虽然个别随机事件在某次试验或观察中可以出现也可以不出现,但在大量重复试验中它却呈现出明显的规律性。假设在相同条件下,独立地重复做n次试验,某随机事件A在n次试验中出现了m次,则比值m/n称为随机事件A在n次试验中出现的频率。当试验重复很多次时,随机事件A的频率m/n就会在某个固定的常数P附近摆动,而且n愈大摆动的幅度愈小。这种规律性称之为统计规律性。频率的稳定性说明随机事件发生的可能性大小是随机事件本身固有的、不随人们意志为转移的客观属性,所以在医学科研中,当n充分大时,就以频率作为概率的近似值,记住P(A)即
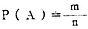
由此可见,频率是就样本而言的,而概率总是从总体的意义上说的。这样,概率就为预计某一事件发生的可能性大小,提供了衡量的尺度。
例如:某病患者40名,用某疗法治疗后,其中35人痊愈,治愈者占治疗人数的35/40,这是频率。因为数量少,这个频率可能波动较大。假如经过长期的大量观察,比如数百、数千例,得到治愈率为70%,我们就可以说,该疗法治愈某病的概率近似值为70%。
又如:某院妇产科在一个月内出生婴儿30名,其中男婴18名,占新生儿数的18/30,这叫频率。大量统计表明,人口中男女的比例基本上是1:1。这是个较稳定的常数,即概率的近似值。于是,在婴儿分娩前,我们就可用它作为尺度,预计是男的概率为1/2(0.5或50%),是女的概率也为1/2(0.5或50%)。
通过以上讨论,可以知道:如果某事件是必然事件,则有m=n,所以必然事件的概率等于1;如果某事件是不可能事件,则有m=0,所以不可能事件的概率等于0;如果某事件是随机事件,则有0<M<N,所以随机事件的概率是介于0与1之间的一个数。某事件的概率愈接近0,表示发生的可能性愈小;愈接受1,表示发生的可能性愈大。
三、随机变量
简单地说,是指随机事件的数量表现。例如一批注入某种毒物的动物,在一定时间内死亡的只数;某地若干名男性健康成人中,每人血红蛋白量的测定值;等等。另有一些现象并不直接表现为数量,例如人口的男女性别、试验结果的阳性或阴性等,但我们可以规定男性为1,女性为0,则非数量标志也可以用数量来表示。这些例子中所提到的量,尽管它们的具体内容是各式各样的,但从数学观点来看,它们表现了同一种情况,这就是每个变量都可以随机地取得不同的数值,而在进行试验或测量之前,我们要预言这个变量将取得某个确定的数值是不可能的。
按照随机变量可能取得的值,可以把它们分为两种基本类型:①离散型随机变量,即在一定区间内变量取值为有限个,或数值可以一一列举出来。例如某地区某年人口的出生数、死亡数,某药治疗某病病人的有效数、无效数等。②连续型随机变量,即在一定区间内变量取值有无限人,或数值无法一一列举出来。例如某地区男性健康成人的身长值、体重值,一批传染性肝炎患者的血清转氨酶测定值等。
四、误差
误差是指实际观察值与客观真值之差、样本指标与总体指标之差。误差可分为系统误差和随机误差。
(一)系统误差 在实际观测过程中,由于仪器未校正、测量者感官的某种障碍、医生掌握疗效标准偏高或偏低等原因,使观察值不是分散在真值两侧,而是有方向性、系统性或周期性地偏离真值。这类误差可以通过实验设计和技术措施来消除或使之减弱,但不能靠概率统计办法来消除或减弱。
(二)随机误差 或称偶然误差,是指排除了系统误差后尚存的误差。它受多种因素的影响,使观察值不按方向性和系统性而随机地变化。随机误差服从正态分布,可以用概率统计方法处理。
在随机误差中,最重要的是抽样误差。我们从同一总体中随机抽取若干个大小相同的样本,各样本平均数(或率)之间会有所不同。这些样本间的差异,同时反映了样本与总体间的差异。它是由于从总体中抽取样本才出现的误差,统计上称为抽样误差(或抽样波动)。抽样误差在医学生物实验中最主要的来源是个体的变异。所以这是一种难以控制的、不可避免的误差。但抽样误差是有一定规律的。研究和运用抽样误差的规律,是根据样本估计总体时所必须领会的基本概念之一,也是医学统计学的重要内容之一。
随机误差中还包括重复误差。它是由于对同一受试对象或检样采用同一方法重复测定时所出现的误差。如用天平称同一个烧杯的重量,重复测定多次,其结果会有某些波动。控制重复误差的手段主要是改进测定方法,提高操作者的熟练程度。重复是摸清实验误差大小的手段,以便分析和减少实验误差。
五、假设检验
亦称显着性检验,其基本原理是先对总体的特征作出某种假设,然后通过抽样研究的统计推理,对此假设应该被拒绝还是接受作出推断。
生物现象的个体差异是客观存在,以致抽样误差不可避免,所以我们不能仅凭个别样本的值来下结论。当遇到两个或几个样本均数(或率)、样本均数(率)与已知总体均数(率)有大有小时,应当考虑到造成这种差别的原因有两种可能:一是这两个或几个样本均数(或率)来自同一总体,其差别仅仅由于抽样误差即偶然性所造成;二是这两个或几个样本均数(或率)来自不同的总体,即其差别不仅由抽样误差造成,而主要是由实验因素不同所引起的。假设检验的目的就在于排除抽样误差的影响,区分差别在统计上是否成立,并了解事件发生的概率。
进行假设检验时,要先建立检验假设(即上述第一种可能,符号是H0)与备择假设(即上述第二种可能,符号是H1),确立检验水准(当检验假设为真,但被错误地拒绝的概率,记作α),通常取α=0.05或α=0.01;然后由样本观察值按相应的公式计算统计量,如X2值、t值等;最后查有关的统计用表确定P值范围(有时也可直接计算P值)作出结论。若P>α,结论为按α所取水准不显著,不拒绝H0,即认为差别很可能是由于抽样误差造成的,在统计上不成立;如果P≤α,结论为按所取α水准显著,拒绝H0,接受H1,则认为此差别不大可能仅由抽样误差所致,很可能是实验因素不同造成的,故在统计上成立。
全部讨论(0)
请在登录后参与讨论...