用秩号代替原始数据后,所得某些秩号之和,称为秩和,用秩和进行假设检验即为秩和检验。其检验假设在两组比较(成对或不成对)时,H0:F(X1)=F(X2),即两总体的分布函数相等,备择假设H1:F(X1)≠F(X2)。本法由于部份地考虑了数据的大小,故检验效力较符号检验大大提高。至于其方法、步骤,不论是查表法或计算法、也都相当简便,现举例说明如下。
一、成对资料的比较
此法由Wilcoxon氏首次提出,故又称Wilcoxon氏法。
处理时可用查表法或计算法,今以例10.3分别说明如下。
查表法步骤:
1.排队,将差数按绝对值从小至大排列并标明原来的正负号,见表10.3第(5)栏,排队后与原豚鼠号已无对应关系。
2.编秩号,成对资料编秩号时较为复杂,要注意三点:
(1)按差数的绝对值自小至大排秩号,但排好后秩号要保持原差数的正负号;
(2)差数绝对值相等时,要以平均秩号表示,如表10.3中差数绝对值为4者共三人,其秩号依次应为2、3、4,现皆取平均秩号3;
(3)差数为0时,其秩号要分为正、负各半,若有一个0,因其绝对值最小,故秩号为1,分为0.5与-0.5,若有两个0,则第二个0的秩号为2,分为1与-1等等。
3.求秩号之和即将正、负秩号分别相加,本例得正秩号之和为68,负秩号之和为10,正负秩号绝对值之和应等于1/2n(n+1),可用以核对,如本例68+10=12/1(12+1)=78,证明秩号计算正确。
4.以较小一个秩号之和(R),查附表12进行判断,该表左侧为对子数,表身内部是较小秩号和,与上端纵标目之概率0.05,0.01相对应,其判断标准是
R>R0.05时P>0.05
R0.05≥R>R0.01时0.05≥P>0.01
P≤R0.01时 P≤0.01
例10.3 请以表10.1资料用秩和检验处理之。
表10.3 豚鼠给药前后灌流滴数及其秩号
| 豚鼠号
(1) | 每分钟灌流滴数 | 按差数绝对值排队
(5) | 秩号 | |||
| 用药前
(2) | 用药后
(3) | 差数
(4) | 正
(6) | 负
(7) | ||
| 1 | 30 | 46 | 16 | -2 | 1 | |
| 2 | 38 | 50 | 12 | -4 | 3 | |
| 3 | 48 | 52 | 4 | 4 | 3 | |
| 4 | 48 | 52 | 4 | 4 | 3 | |
| 5 | 60 | 58 | -2 | -8 | 6 | |
| 6 | 46 | 64 | 18 | 8 | 6 | |
| 7 | 26 | 56 | 30 | 8 | 6 | |
| 8 | 58 | 54 | -4 | 10 | 8 | |
| 9 | 46 | 54 | 8 | 12 | 9 | |
| 10 | 48 | 58 | 10 | 16 | 10 | |
| 11 | 44 | 36 | -8 | 18 | 11 | |
| 12 | 46 | 54 | 8 | 30 | 12 | |
68 R=10
将表中10.1中用药前后的数据求出差数,并按差数绝对值排队,结果见表10.3第(5)栏。再编秩号,为计算方便,正、负秩号分列两栏,见表10.3第(6)、(7)栏。
上例,n=12,∣R∣=10,查附表12得
R0.05=14R0.01=7
今R0.05>R>R0.01,故0.05>P>0.01,在概率0.05水平上拒绝H0,接受H1,即用药前后的相差是显著的,给药后每分钟灌流滴数比用药前增多了。
附表12中只列有n≤25时的临界值。当n值较大时亦可采用计算法。
计算法步骤:
在计算法时,对差数的排队,编秩号及求秩号之和同查表法,不同的是求得秩号之和以后的算,所用公式是:
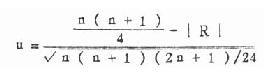
u0.05=1.96u0.01=2.58 (10.5)
式中n为原始资料中数据的对子数,R为正秩号之和或负秩号之和,为计算方便,通常取绝对值较小的秩号之和为r 。
本例,n=12,R=-10,代入得:
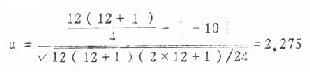
U0.05<U<0.01,故0.05>P>0.01,在α=0.05水准上拒绝H0,接受H1,结论与查表法相同。
据研究,当n大于10时,上式算得的u近似正态分布,故计算法只用于n值较大时。
因本例资料接近正态分布,故曾用t检验的个别比较方法处理过,结果是:t=2.653 0.05>P>0.01,与秩和检验结论相同,但与符号检验结论不同(χ2=2.083,P>0.05),说明符号检验的检验效率比秩和与t检验都要低,比较粗糙,而秩和检验的效率与t检验较接近。
二、两组资料的比较
此法又称为wilcoxon氏两样本法。
处理时也可用查表法或计算法,今以例10.4分别说明之。
查表法步骤:
1.各自排队,统一编秩号,即将两组数据分别从小到大排列,但编秩号时要两组统一进行,凡分属于两组的相等数据用平均秩号,如本例0.042共三个,取平均序号皆为8。
2.令较小样本秩号之和为r ,例数为n1。
3.计算R',公式为:
R'=n1(n1+n2+1)-r (10.6)
R'是同一个样本资料,当秩号倒排(即由大至小)时较小样本秩号之和。
4.以R和R'两秩号之和中较小者与附表13中R的临界值比较,以作出判断,其标准仍是:
R>R0.05时 P>0.05
R0.05≥R>R0.01时 0.05≥P>0.01
P≤R0.01时 P≤0.01
例10.4 请以表10.2资料用本法处理之。
表10.4 九名健康人与八名铅作业工人的尿铅值(mg/L)
| 健康人 | 秩号 | 铅作业工人 | 秩号 |
| 0.001 | 1 | 0.042 | 8 |
| 0.002 | 2 | 0.042 | 8 |
| 0.014 | 3 | 0.048 | 10 |
| 0.020 | 4 | 0.050 | 11 |
| 0.032 | 5 | 0.082 | 14 |
| 0.032 | 6 | 0.086 | 15 |
| 0.042 | 8 | 0.092 | 16 |
| 0.054 | 12 | 0.098 | 17 |
| 0.064 | 13 | ||
| n2=9 | 54 | n1=8 | R=99 |
先将本表10.2中两组数据各自排队并统一编秩号,结果见表10.4。
较小样本为铅作业工人组,n1=8,R=99,代入式(10.6)
R'=8(8+9+1)-99=45
R与R'两者中以R'较小,故以P'值与附表13数值比较,得R0.05=51,R0.01=45;今R'=R0.01,故P=0.01,在α=0.05水平上拒绝H0,接受H1,差别显著,故铅作业工人尿铅值比健康人高。
计算法步骤:
两组资料比较时,也可用计算法。用计算法时,对两组数据各自排队、统一编秩号同查表法,不同的是求得秩号之和以后计算,公式是:

u0.05=1.96u0.01=2.58 (10.7)
为便于计算和前后符号一致,n1作为较小样本例数,R为较小样本的秩和,n2则为较大样本的例数。
本例n1=8,R=99,n2=9代入公式得:
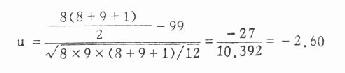
今∣u∣>u0.01,故P<0.01,在α=0.01水准上拒绝H0接受H1,其结论同查表法,
据研究,当n1、n2都大于8时,算得的u近于正态分布,若例数太少,则以查表法更为精确。
本例如用t检验的团体比较处理,则t=3.169,P<0.01,二者结论一致,但与符号检验结论不同(χ2=2.930,P>0.05)同样说明符号检验较粗糙,检验效率低,而秩和检验与t检验的结论较近。
三、两组等级资料的比较
等级资料又称为半计量资料,当两组等级资料比较时,用秩和检验来比较其相差是否显着比用χ2检验要恰当。两组等级资料,通常例数都较多,故一般都用计算法,其步骤与两组资料的秩和检验相似,不同的是要求各等级的平均秩号,为此,先要求得各等级的秩号范围。今举例10.5说明之。
1.求各等级的平均秩号。为此,先要求出各等级的秩号范围,如等级“-”共18+8=26例,共秩号范围自1~26。要注意的是各等级的秩号范围必须紧相联接。最后一组秩号范围的上限一定等于两组例数之和。求得各等级秩号范围后,再求其下限和上限的平均,即可算得平均秩号,如等级“一”的平均秩号为(1+26)/2=13.5。余类推。
2.求出R及其n1,为计算方便,把例数少的正常人组的秩号之和作为R其例数为n1得R=308,n1=20,n1=32
3.代入式(10.7)得u值,即可作结论。
例10.5,今有20名正常人和32名铅作业工人尿棕色素定性检查结果如下表10.5,试问其相差是否显著?
表10.5 20名正常人和32名铅作业工人尿棕色素定性检查结果
| 尿棕色素定性结果 | 正常人 | 铅作业工人 | 合计 | 秩号范围 | 平均秩号 | 例数较小组的秩和 |
| - | 18 | 8 | 26 | 1—26 | 13.5 | 243 |
| + | 2 | 10 | 12 | 27—38 | 32.5 | 65 |
| ++ | — | 7 | 7 | 39—45 | 42.0 | — |
| +++ | — | 3 | 3 | 46—48 | 47.0 | — |
| ++++ | — | 4 | 4 | 49—52 | 50.5 | — |
n1=20 n2=32 R=308
代入式(10.7)
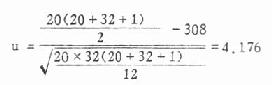
u0.01=2.58,今u>u0.01,故P<0.01,在α=0.01水准上拒绝H0,接受H1。两组相差显著,铅作业工人尿棕色素比正常人为高。
四、多组资料的比较
多组资料的比较也是从排秩号开始,但不是直接用秩和进行检验,有的书籍称之为秩检验(rank test),以示与秩和检验有别,其检验假设也较复杂:在处理完全随机设计的资料时,H0:F(X1)=F(X2)=F(X3)=……,即比较的各样本所对应的各总体的分布函数相等,H1:各总体的分布函数不相等或不全相等;在处理随机单位组设计的资料时,H0:P(χij=r)=1/n,即内组各秩号r之概率相等,都是1/n(r=1,2,……,n)而H1为:P=(χij=r)≠1/n。
因不同实验设计所得资料的处理也有别,故下面分别举例说明之。
(一)完全随机设计所得资料的比较
用的方法是单因素多组秩检验,称为Kruskal-Wallis氏法,或H检验。其计算步骤如下。
1.各自排队,统一编秩号。即将各组数据在本组内从小到大排队,见表10.6各含量栏,再将各组数值一起考虑编出统一秩号,见表10.6各“秩号”栏,分属不同组的相同数值用平均秩号;
2.求各组秩号之和R1以及各组数n1:
3.代入下式计算H值:

(10.8)
式中N为各组例数之和,Ri和ni为各组的秩号之和以及例数:
4.查表作结论
当比较的组数多于三组,或组数虽只有三组但每组例数大于5时,H值的分布近于自由度等于组数-1的χ2分布,故可用对应的χ2值作界值。当三组比较时每组例数均不超过5时,H值与χ2值有较大偏离,此时可查附表14,直接查得H0.05和H0.01。
例10.6 雄鼠20只随机分为四组,第1、2组在皮肤上涂用放射性锡(Sn113)标记的三乙基硫酸锡,涂后将皮肤暴露于空气中;第3、4组涂药后用密闭小玻璃管套使皮肤与外界空气隔开,三小时后杀死,测肝中放射物,结果如表10.6,试比较各组含量间有无显著相差?
表10.6 白鼠皮肤涂药后,肝中放射性Sn113的含量
| 涂干药后敞开 | 涂湿药后敞开 | 涂干药后密闭 | 涂湿药后密闭 | ||||
| 含量 | 秩号 | 含量 | 秩号 | 含量 | 秩号 | 含量 | 秩号 |
| 0.00 | 1 | 1.82 | 11 | 0.66 | 5 | 3.67 | 14 |
| 0.42 | 2.5 | 2.79 | 12 | 0.71 | 6 | 4.46 | 16 |
| 0.42 | 2.5 | 3.07 | 13 | 0.75 | 7 | 4.51 | 18 |
| 0.59 | 4 | 4.19 | 15 | 0.83 | 8 | 5.07 | 19 |
| 0.97 | 9 | 4.47 | 17 | 1.49 | 10 | 6.02 | 20 |
| Ri | R1=19 | R2=68 | R3=36 | R4=87 | |||
| ni | n1=5 | n2=5 | n3=5 | n4=5 | |||
各组资料各自排队,统一编秩号,以及求各组的秩号之和Ri和例数ni见表10.6
代入式(10.8)得
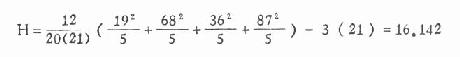
本例组数为4(>3),查χ2值表,ν=4-1=3,得χ20.05,3=7.81,χ20.01,3=11.34,今H>χ20.01,3,故P<0.01,在α=0.01水准上拒绝H0,接受H1,即各组肝中放射性Sn113含量差别显著。
(二)随机单位组设计所得资料的比较
用的方法是双因素多组秩检验,即Friedman氏法。
处理这种资料时可分成两步,对两个因素分别进行检验。现用例10.7说明其计算步骤:
先比较四种防护服对脉搏的影响
1.将穿四种防护服的每一受试者的脉搏数从小到大编秩号,当数值相等时用平均秩号,见表10.7各秩号栏。
2.求各防护服组秩号之和Ri
3.代入式10.9求H值

(10.9)
式中t(treatment)为处理组数,b(block)为单位组数。
4.查表作结论
当t>4或t=4且b>5或t=3且b>9时,H值的分布近于自由度ν=t-1时的χ2分布,故可查相应的χ2值与H值比较作出判断:如t、b不能满足上述条件,则所算得的H值与χ2分布有较大偏离,需查附表15作判断。
例10.7 受试者5人,每人穿四种不同的防护服时的脉搏数如表10.7,问四种防护服对脉搏的影响有无显著差别?又五个受试者的脉搏数有无显著差别?
表10.7 比较穿四种防护服时的脉搏数(次/分)
| 受试者 | 防护服A | 防护服B | 防护服C | 防护服D | ||||
| 编 号 | 脉搏 | 秩号 | 脉搏 | 秩号 | 秩号 | 秩号 | 脉搏 | 秩号 |
| 1 | 144.4 | 4 | 143.0 | 3 | 133.4 | 1 | 142.8 | 2 |
| 2 | 116.2 | 2 | 119.2 | 4 | 118.0 | 3 | 110.8 | 1 |
| 3 | 105.8 | 1 | 114.8 | 3 | 113.2 | 2 | 115.8 | 4 |
| 4 | 98.0 | 1 | 120.0 | 3 | 104.0 | 2 | 132.8 | 4 |
| 5 | 103.8 | 2 | 110.6 | 4 | 109.8 | 3 | 100.6 | 1 |
| 秩秩号和Ri | 10 | 17 | 11 | 12 | ||||
t=4b=5
排队、编秩号、求各比较组的Ri见表10.7所示。
将表10.7中各数代入式10.9,得
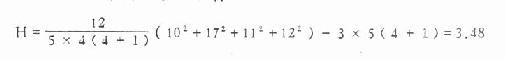
本例t=4,b=5查附表15,得H0.05=7.80,今H>H0.05,故P>0.05,在α=0.05水准上接受H0,无显著差别,故四种防护服对脉搏的影响无显著差别。
再比较五名受试者的脉搏数:
将数据列出(同表10.7),但秩号是按每种防护服中受试者脉搏的数值从小到大编定,然后求出各受试者秩号之和R1,详细见表10.8
表10.8 比较五名受试者的脉搏数
| 受试者 | 防护服A | 防护服B | 防护服C | 防护服D | Ri | ||||
| 编 号 | 脉搏 | 秩号 | 脉搏 | 秩号 | 脉搏 | 秩号 | 脉搏 | 秩号 | |
| 1 | 144.4 | 5 | 143.0 | 5 | 133.4 | 5 | 142.8 | 5 | 20 |
| 2 | 116.2 | 4 | 119.2 | 3 | 118.0 | 4 | 110.8 | 2 | 13 |
| 3 | 105.8 | 3 | 114.8 | 2 | 113.2 | 3 | 115.8 | 3 | 11 |
| 4 | 98.0 | 1 | 120.0 | 4 | 104.0 | 1 | 132.8 | 4 | 10 |
| 5 | 103.8 | 2 | 110.6 | 1 | 109.8 | 2 | 100.6 | 1 | 6 |
t=5b=4
将表10.8 所得各数据代入式10.9得
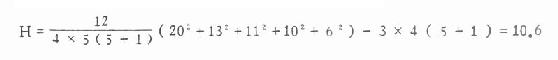
此处t>4,故查ν=5-1=4时的χ2值表,得:χ20.05,4=9.49,χ20.01,4=13.28,今χ20.05,4<H<X20.01,4,故0.05>P>0.01,在α=0.05水准上拒绝H0,接受H1,差别显著;即五名受试者脉搏数相差显著,1号受试者最高,5号受试者最低。
五、多组资料间的两两比较
当多组间的差别显着时,则需进一步判断那些组之间的差别有显着性,这个问题的解决方法与第八章第二节中的多个均数间的两两比较很相似,在例10.6四个实验组涂放射性锡的例子中,结果为H>χ20.01,3,P<0.01,现以此为例,进一步作各组两两间比较,步骤如下:
1.将各组秩和从大到小依次排队,并求得两两间的相差,见表10.9
2.计算标准误,计算公式是:

(10.10)
式中σ为任意两个秩和之差的标准误,n为各组例数,a为处理数,此式要求各组例数相等,
3.查q值表定界限作结论
仍查方差分析时用的q值表,v→∝
各q值须与处理数相同的标准误相乘,如处理数为2的q值要乘以处理数为2时的标准误,2.77×6.77=18.75,3.64×6.77=24.64等,余类推。
例10.6资料两两间比较如下:
表10.9 每两组秩和之间的相差及其显著性
| 组别 | 秩和Ri | Ri—19 | Ri—36 | Ri—68 |
| 涂湿药后密闭 | 87 | 68** | 51** | 19* |
| 涂湿药后敞开 | 68 | 49** | 32** | |
| 涂干药后密闭 | 36 | 17 | ||
| 涂干药后敞开 | 19 |
计算标准误:n=5,用式10.10
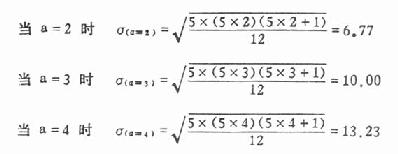
查q值表,得:
| 处理数 | 2 | 3 | 4 |
| q0.05,∞ | 2.77 | 3.31 | 3.63 |
| q0.01,∞ | 3.64 | 4.12 | 4.40 |
| q0.05,∞σ | 18.75 | 33.10 | 48.02 |
| q0.01,∞σ | 24.64 | 41.20 | 58.21 |
两两比较后的结论见表10.9所示,结合起来看,结论是:涂湿药的比涂干药肝中放射性Sn113含量要高,涂湿药中,密闭的比敞开的含量高。
全部讨论(0)
请在登录后参与讨论...