一、估计样本含量的意义及条件
我们在第一节里曾提到重复的原则。所谓重复,是指各处理组(对照在实验研究中也被看作是一种处理,而且是必不可少的)的受试对象都应有一定的数量,例数不能太少,所以在抽样调查、临床观察或实验研究中,首先总要考虑样本含量(或叫样本大小)问题。样本太小,使应有的差别不能显示出来,难以获得正确的研究结果,结论也缺乏充分的依据;但样本太大,会增加实际工作中的困难,对实验条件的严格控制也不易做到,并且造成不必要的浪费。所以这里所说的样本含量估计,系指在保证研究结论具有一定可靠性的条件下,确定最少的观察或实验例数。
但是,样本含量又是个比较复杂的问题。要讲清在各种情况下估计样本含量的方法和原理,那是很繁杂的。而且,不同的参考书上介绍的计算公式和工具表往往不一样,以致同一问题所得的结果也可能有出入。所以,不论按哪种公式或工具表求得的结果,也只能是个近似的估计数。
估计样本含量,必须事先明确一些条件与要求:
(一)根据研究目的与资料性质,要先知道一些数据。例如要比较几组计数资料,先要知道百分数或率;要比较几组计量资料,先要知道平均数及标准差。这些数据可从以往的实践,预备试验的结果、兄弟单位的经验或文献资料里得来。
(二)确定容许误差。由于抽样误差的影响,用样本指标估计总体指标常有一定的误差,因而要确定一个样本指标与总体指标相差所容许的限度。此值要求越小,所需例数就越多。
(三)确定把握度(1—β)。β是第二型错误的概率;而1—β的意思是:如果两组确有差别,则在每100次实验中平均能发现出差别来的概率。把握度可用小数(或百分数)表示,一般取0.99、0.95、0.90、0.80、0.50。要求把握度越高,则所需例数直多。
(四)确定显著性水平,即第一型错误的概率(α)。这就是希望在α=0.05的水准上发现差别,还是希望在α=0.01的水准上发现差别。α越少,所需例数越多。
此外,估计样本含量时还应当根据专业知识确定用单侧检验或双侧检验。同一实验,若既可用单侧检验又可用双侧检验,则前者所需例数要少些。
二、用计算法估计样本含量
我们运用前面学过的某些假设检验公式,就可以进行样本含量的计算。下面仅举两例略作介绍。这里的公式仅适用于α=0.05,1—β=0.50。而且都是双侧检验。
(一)两个率比较时样本含量的计算 令n为每组所需例数,P1、P2为已知的两个率(用小数表示),P为合并的率,当设两组例数相等时,即P=(P1+P2)/2。q=1=p,则
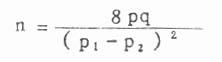
(11.1)
例11.5 据某院初步观察,用甲、乙两种药物治疗慢
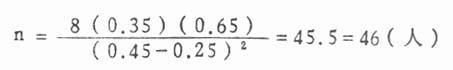
性气管炎患者,近控率甲药为45%,乙药为25%。现拟进一步试验,问每组需观察多少例,才可能在α=0.05的水准上发现两种疗法近控率有显著相差?
本例P1=0.45,P2=0.25,P=(0.45+0.25)÷2=0.25,q=1-0.35=0.65,代入式11.1
每组需观察46人,两组共观察92人,注意:例数问题不同于一般数学计算中的四舍五入,凡是有小数的值,应一律取稍大于它的正整数,如本例45.5取46,若为45.1也应取46。
(二)个别比较t检验样本含量的计算 令n为所需样本数,S为差数的标准差,X为差数的均数,t0.05O为t值表上相当于P=0.05的t值,4为n足够大时t20.05=1.962的数,则
大样本
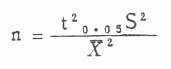
(11.2)
小样本
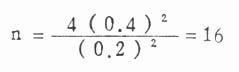
(11.3)
例11.6 用某药治疗胃及十二指肠溃疡病人,服药四周后胃镜复查时,患者溃疡面平均缩小0.2cm2,标准差为0.4cm2,假定该药确能使溃疡面缩小或愈合,问需多少病人作疗效观察才能在α=0.05的水准上发出用药前后相差显著?
本例X=0.2,S=0.4,先代入式(11.2)
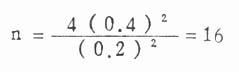
由于n<30,故用式(11.3)重算。当n=16,ν=16-1=15,t0.05=2.131,
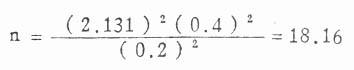
当n=19(略大于18.16),ν=19-1=18,t0.05=2.101
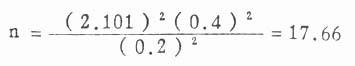
当n=18,ν =18-1=17,t0.05=2.110
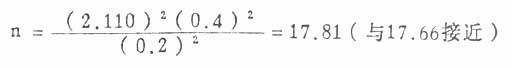
故至少需用18人作疗效观察。
三、用查表法估计样本含量
当要求平均有80%、90%以上的机会能发出相差显着或非常显着时,计算公式比较复杂,数理统计上已编制成工具表,一查便得,附表19只是其中的一部分。我们仍以前面的例题来介绍这些表的用法。
(一)两个率比较时所需样本含量 对于两个率的比较,单侧检验可查附表19(1),双侧检验查附表19(2)
仍用例11.5来说明。本例P1=45%,P2=25%,δ=45%-25%=20%,设α=0.05,把握度为0.80。如果已知甲药疗效不可能低于乙药,可用单侧检验,查附表19(1)。我们从“较小率”栏中找到25横行,再从上方找到δ=20直行,基相交处,读上行数字得69,即每组最少需要69例,两组共需138例。
如果两个率(或百分数)都超过50%,怎样使用这个表呢?假定甲组阳性率是80%,乙组阳性率是65%,两组阳性率相差15%。这时先求两组的阴性率,于是甲组阴性率为20%,乙组阴性率为35%,两组阴性率相差仍为15%。若用双侧检验,我们查附表19(2),从“较小率”栏找到20横行,再从上方找到δ=15直行,其相交处上行数字为135,即每组需检查135例(两组共270例)将有80%的机会在α=0.05的水准上发现两组阳性率相差显著。
若表中查不到题中的“较小率”及δ,可用最接近的值或内插法求n,但宁可使n偏大,以免估计的样本含量偏少。
(二)个别比较t检验所需的样本含量 这是配对比较,应查附表20。使用该表时,先要求出差数的总体均数μ与总体标准差σ之比,即δ=μ/σ,当μ与σ未知时,可分别用X与S作为估计值。
仍用例11.6来说明,本例X=0.2,S=0.40,故δ=μ/σ=0.2/0.4=0.5。若设α=0.05,1—β=0.90,用双侧检验,查附表得20,得n=44,即需观察44例病人。若设α=0.05,1—β=0.50,则n=18,同计算法结果一致。
(三)两个均数比较所需样本含量 应查附表21。先要求出两总体均数之差与总体标准差这比,即δ=(μ1-μ2)/σ。若μ1及μ2未知时,可分别以X1及X2估计之;σ未知时,可以合并标准差S估计之。
例11.7 某职业病防治所用两种疗法治疗矽肺患者,一个疗程后,患者血清粘蛋白下降值甲疗法平均为2.6(mg%),乙疗法平均为2.0(mg%,)两种疗法下降值之合并标准差为1.3(mg%)。若发现两组疗效相差显著,每组至少应观察多少病人?
本例X1=2.6,X2=2.0,S=1.3,故δ=(μ1-μ2)/σ=(2.6-2.0)/1.3=0.46。若设α=0.05,1—β=0.50,用双侧检验,查附表21,δ=0.46查不到。在这种情况下,可用邻近而略小的δ值代替,或用内插法估计。本例若查δ=0.45,得n=39,即每组需要39例,两组共需78例。若用内插法计算,当δ=0.45时所需例数是39,δ=0.50时所需例数是32,所以δ=0.46时所需例数是:
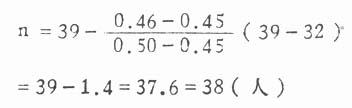
答案是:每组需要至少观察38例,两组共需观察76例。
全部讨论(0)
请在登录后参与讨论...